Now there is one data structure in Houdini that happens to be perfect for what we need :
A heightfield is a grid, just instead of being a polygonal grid, it's a volumetric grid. To be more precise it's a 2d Volume. Each voxel of the grid contains a floating point number that corresponds to the height of the visual representation of that voxel.
Let's get familiar with HF first in Houdini.
In a SOP context drop a HeightField SOP node , set size to 100 , 100 and middle click on it to check the info.
You can see the node generates 2 volumes: 'height' and 'mask'.
In order to get familiar with these new concepts let's now drop a Volume Wrangle and enter the following code in the "VEXpression" field.
I don't want to go too deep into HF (please make sure to watch the Masterclasses I mentioned before), but there are a couple of important facts to keep in mind:
Ok enough about HeightFields. Let's dive into the sand algorithm.
In PART 1 I named each cell 'stack'. Since we're now dealing with Volumes, I'll use the term 'voxel' to refer to the stacks.
First off we need to create an environment that will allow us to play with HeightFields. We'll use the Mask volume (generated by the HeightField SOP) as a debugging tool, as we have already done previously.
Cool, let's create a new Geo context, and name it "sandpile_VEX". Dive inside and create the following.
heightfield1 node generates a 20x20 sized grid. Grid Spacing is 1, meaning that there is 1 voxel per unit. If we put 0.5 in there we would have twice the number of voxels. This parameter is a very quick way to increase the HF resolution.
So we have a total of 400 voxels, and the volume indices are as follow:
i@ix = [ 0:19 ]
i@iy = [ 0:19 ]
heightfield_noise1 node modifies the 'height' field using a noise function. This is a quick way to create an initial sand distribution.
In the view port you should see something similar to this.
In PART 1 we split the algorithm in 2 steps. Let's work on step 1.
STEP 1
For each voxel (or stack), find out if any of the 4 adjacent voxels is lower by a certain amount (let's say 1).
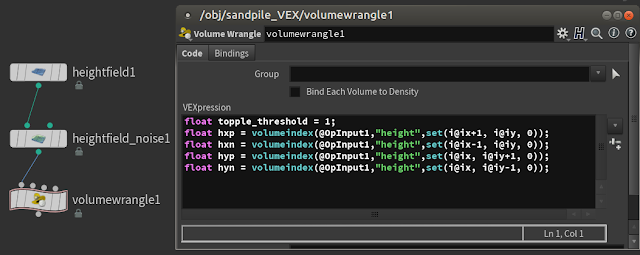
Drop a Volume Wrangle node and write the following code in the parameter 'VEXpression'
In the first line we set the topple_threshold. If the current voxel is taller than the adjacent voxels by a height value bigger than 'topple_threshold', it means the current voxel should topple. But don't worry, we'll use this variable later.
Now, the biggest advantage of using volumes as a data structure is that I can find the adjacent voxels very very quickly. The grid position of the 'current voxel' is given by i@ix and i@iy. So if I want to access the voxel to the left, right , top or bottom of the current voxel all I need to do is add or subtract a 1 here and there.
The following 4 lines read the 'height' value from the 4 voxels adjacent to the current voxel.
We'll ignore the voxels in the corners.
Let's translate the following line in English :
Dear Houdini, please read the content of the node attached the first input (@OpInput1), which I assume is a volume. But since there are 2 volumes flowing through that connection ('height' and 'mask') I want to be more specific : the volume I am interested in is named "height", but hey ... not the whole thing. No way. I want the content of one voxel, and more specifically the one sitting at the index ( ix+1 , iy , 0 ). Once you get that data contained in that voxel, please put it in a float variable named 'hxp'.
@OpInput1 is just a fancy way of saying "node input 0". You can write directly 0 in there, and it will still work perfectly. I prefer to use the fancy form cause it's more descriptive for my lazy brain.
Ok now the variables hxp, hxn, hyp, hyn contain the height value of the 4 adjacent voxels. At the moment we're doing nothing with this data.
Let's add some more Vex code:
The purpose of the new 4 lines is to flag which of the adjacent voxels is a candidate for the current voxel to topple towards to.
Let's make an example:
Let's assume the height of the current voxel (f@height) is 3.
Let's assume the height of the adjacent voxel on the positive x (hxp) is 6.
And we know that topple_threshold is 1.
3 - 6 = -3
is -3 bigger than 1 ? False . Then txp = False (or 0).
Meaning, the current voxel cannot topple towards the adjacent voxel on the positive x, cause that voxel is actually taller ! Actually that voxel could topple towards the current, but that will be evaluated in some other iteration of the Volume Wrangle node loop.
Another example:
Let's assume the height of the current voxel (f@height) is 3.
Let's assume the height of the adjacent voxel on the negative y (hyn) is 1.
And we know that topple_threshold is 1.
3 - 1 = 2
is 2 bigger than 1 ? True . Then tyn = True (or 1).
This means that the current voxel could topple towards the adjacent voxel on the negative y, cause it's lower than the threshold value.
Once we collect all the values for txp, txn, typ, tyn we can put this into an array.
The line with hdiff[] is initializing the array to an array of 4 integers. All zeros to start.
Then I'm replacing each element of the array with txp ... tyn, that we know can be only 0 or 1.
Please note that in this moment we just established an important convention. Meaning that the first element in the array corresponds to the upper voxel (yp). The 3rd element of the array corresponds to the lower voxel (yn) and so on. We could have chosen a different convention of course, I just like starting from top and going clockwise. Feel free to go crazy with it, just remember to maintain the same convention later.
 |
| Fig 1 |
In the very last line I sum all the values contained in the array and store it in a new variable called 'topple_candidates'. This variable ultimately answers the most important question : "is the current stack going to topple ?"
If this variable is zero, it means that the array is composed by 4 zeroes, which in turn means that none of the adjacent voxels is a candidate for the current stack to topple.
In other words, if this variable is bigger than zero, the current stack is unstable. And it's really easy now to color code those voxels using the grid 'mask'.
All we need to do is add the following line :
f@mask = topple_candidates > 0;
Which brings the entire code to this :
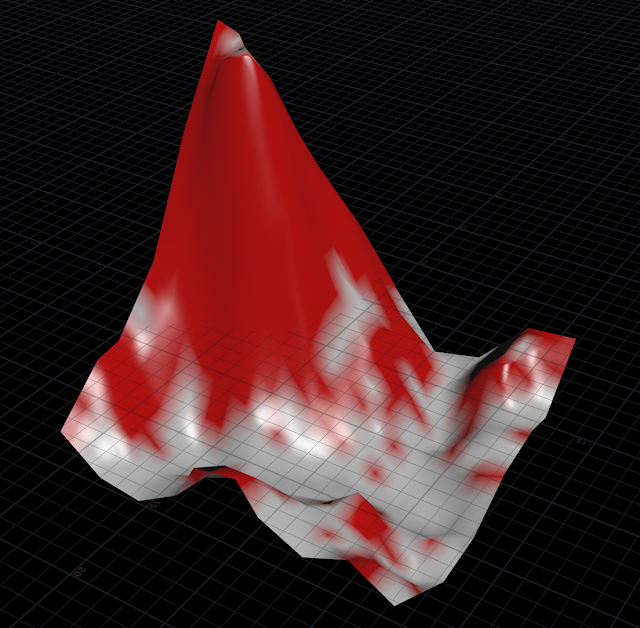
Now if you look at the view port, you'll probably see this :
Yes it does look like a napkin full of blood. Let's try to ignore that.
This is a very comforting result : note how the voxels that lie on the ground area are all white, cause none of those have adjacent voxels that are much lower. Those white voxels are stable and will not topple. The red voxels instead are on steep slopes and it makes a lot of sense that they might topple down.
But there is one issue we need to resolve before moving to the next step: at the moment if you change the resolution of the grid ( heightfield1 -- Grid Spacing Parameter) you'll notice that the toppling areas (in red) shrink or grow.
This is not what we want. We want to be able to develop our algorithm on a fast grid (say 20x20), and once we're happy with it, move to a way higher res grid without fearing that the result will change. In other words we need to make our system resolution independent.
First off let's try to understand why this is happening.
When we change the resolution of the grid , we effectively change the size of each voxel. But the 'topple_threshold' height is always 1. Somehow we need to tie grid spacing with topple_threshold.
when grid spacing becomes smaller, that means that the voxel becomes smaller, consequently even topple_threshold should become smaller.
grid_spacing ---- voxel size ---- topple_threshold
So the parameter Grid Spacing and the variable 'topple_threshold' seem to be connected by a linear dependency. Let's just multiply those, and use the result as our new 'adaptive' topple_threshold.
First off I parametrized a new variable called 'topple_threshould_mult', and created a new parameter called 'grid_spacing' linked to the parameter 'grid_spacing' on the heightfield1 node.
At this point I can finally calculate the new 'topple_threshold' :
topple_threshold = grid_spacing * topple_threshold_mult ;
Now the red areas will stay consistent even if we change the resolution, on top of that we've an additional slider to change the toppling threshold !
Switch to a more decent resolution, something that will show some cool detail. On the node "Heightfield1" set the parameter Grid Spacing to 0.05.
Great !
Now let's get back for a moment to the variable 'topple_candidates'.
We said that if this is bigger than 0 it means the current stack will topple.
Now the question is "in which direction will it topple ?".
In PART 1 I decided to choose the toppling direction randomly. Note that I made this choice cause it's the simplest one. More elaborate solutions would be to choose the toppling direction based on a vector (which could be wind, or forces like mm .. collisions / proximity with other objects). For the sake of simplicity we'll go for the random route, but please feel free to experiment with other solutions on your own.
We need to choose one of the non-zero elements in the array randomly and store the index in an additional grid that we'll name 'dropdir'.
Let's abstract the problem here :
I have an array of 1s and 0s
example :
A = [ 0 , 1 , 0 , 1 ]
I want my code to *randomly* return 1 or 3 (the indices of the array that correspond to 1s).
another example :
A = [ 1 , 0 , 0 , 1 ]
I want my code to *randomly* return 0 or 3 (the indices of the array that correspond to 1s).
another example :
A = [ 0 , 0 , 1 , 0 ]
I want my code to always return 2 (the only index of the array that correspond to 1).
A really simple solution is the following (if you find a smarter and/or faster solution please please let me know):
- count how many 1s are present in the array (we already have this value, it's the variable 'topple_candidates')
Example :
if the array A = [ 0 , 1 , 0 , 1 ] , topple_candidates = 2
if the array A = [ 1 , 0 , 1 , 1 ] , topple_candidates = 3
- if the array A = [ 0 , 0 , 0 , 0 ] , topple_candidates = 0
- find a random integer number between 0 and topple_candidates ( let's call it R )
if topple_candidates = 2 , R = 1 or 2
if topple_candidates = 3 , R = 1 , 2 or 3
if topple_candidates = 1 , R = 1
- loop over the array until I find as many 1s as R
- store the array index in 'dropdir'
Ok first off we need to create an additional grid named 'dropdir'. As we just mentioned earlier each voxel of this grid will contain a number between 0 and 3. This number will give an indication of the toppling direction, according to the convention established in fig.1.
Modify your network this way:
In other words I'm duplicating the field 'height', renaming it to '_toppledir' (I like to ad a leading underscore to temporary data) and merging it back with the other 2 fields 'height' and 'mask'. The 'primitive1' node will disable the visibility of this new grid. For now I disabled this node cause we want to see what happens on this grid when we start storing values. We'll hide it after we are sure it's working properly.
In the view port you should see something like this
Now if you middle click on the
merge1 node you should see 3 grids.
- height - the bloody napkin, now more similar to a bloody mountain
- mask - not visible as a grid, but visible as red mask on the 'height' field
- _toppledir - a copy of the height field, but completely flat since all the voxels have a zero value.
Now modify the code in volumewrangle1 this way:
( I know , you hate me cause you can't copy and paste the code. But guess what, I did it on purpose ! 😼 I want you to write it all cause I want you to get used to code in VEX, opposed to become a copy and paste black belt. On top of that formatting code with Blogger is a real pain ... )
Let's quickly go over the new code.
First off, the whole new code is almost entirely enclosed in a big if-statement: if topple_candidates is zero, we mark that voxel as stable ( or -1 ) and we move on to the next voxel.
Otherwise ...
first off we set a random number 'rnd' between 0.0 and 1.0.
let's focus on this line :
int r = 1 + floor ( rnd * topple_candidates )
The first thing to keep in mind is that the function floor( a ) returns the integer part of a.
For instance :
floor(0.3) will return 0
floor(1.543) will return 1
floor(12.543) will return 12
now ...
(rnd * topple_candidates) is just a way to re-map a number that is in the range between 0.0 and 0.99999... to a number in a range between 0.0 and topple_candidates-1.
Floor will return the integer part of it, which is ... 0 - (topple_candidates-1)
But, remember that the purpose here is to create a random number between 1 and topple_candidates cause we want to use this number (r) as a counter ... so we just need to add 1. Hence ...
int r = 1 + floor ( rnd * topple_candidates )
In the for-loop below I start looping over the 4 elements of the array hdiff[]. This array will have at least one 1, otherwise we would have been kicked out of the if-statement earlier.
In this loop , a variable 'c' will be increased every time we meet a 1 in the array. As soon as 'c' reaches the desired count 'r', we have found the index, and we can exit the loop (break statement).
All we need to do now is store the index in '_toppledir' !
Now if you look at the view port you'll see something weird ...
... and kinda beautiful.
The weird looking spiky thing is the '_toppledir' grid. This grid should contain numbers between -1 and 3. In fact, if you switch to the front view , you'll notice exactly that !
On top of that, if you look closely, you'll notice the following:
- areas corresponding to white areas in the 'height' grid are flat and at level -1
- areas corresponding to red areas in the 'height' grid are always higher than -1
- if you scrub the frame in the timeline, the peaks should change randomly (cause the variable 'rnd' is dependent on @Time) , but not the ones in the white areas of the 'height' field.
- there are a few flat areas that don't correspond to white areas of the 'height' field ! Those should correspond to slopes where there can be only one toppling direction. These areas will be flat, yes, but higher than -1 level.
Cool.
The good news is that Step 1 is done !
Let's rename volumewrangle1 to step1.
Oh and let's store the value calculated for 'topple_threshold' in a detail attribute, on the geometry itself. This way I don't need to calculate it again in Step 2.
The VEX line above will use the command 'setdetailattribute' to create a detail attribute
A detail attribute is simply a per-object attribute, opposed to a per-point, per-vertex, per-prim attributes.
I generally use detail attributes to store values that exist for the whole object. They're super convenient cause they're kinda similar to parameters, but attached to the geometry itself, so they flow along the whole graph and you can access it from everywhere. On top of that, they're very light since there's only one per object, and the size is independent on how heavy is the geometry.
Why not call them 'object attributes' instead of 'detail attributes' ? MMMmmm ... well ...
STEP 2
Let's quickly recap.
At this stage we've 3 volumes:
- Height : contains our sand. It's a 2d volume. Each voxel contains the height of the corresponding stack of sand.
- _dropdir : contains the info about which stack is stable or unstable. On top of that, for those who are unstable, it even tells us in which direction they'll topple. More specifically (check Fig.1) :
- -1 : stable
- 0 : topple up
- 1 : topple right
- 2 : topple down
- 3 : topple left
- Mask : used only for debugging purpose. At the moment it flags red all the unstable Height voxels.
So, well ... we know everything. All we need to do is actually do the toppling thing.
All we need to do is this:
For each voxel V in the grid 'Height':
- find which of the 4 adjacent voxels is marked to topple towards V and increase V's Height accordingly.
Example:
Looking at V's 4 adjacent voxels, two of them will topple on V. One is the voxel on the right that contains the value -3 (which, according to out convention, means it's going topple left), and the other is the voxel down that contains the value 0 (which , according to our convention, means it's going to topple up). So a total of 2 'grains of sand' will land on V, increasing it's Height.
- if V itself is not stable (meaning that it will topple on one of its 4 adjacent vectors) decrease V's 'Height" accordingly. In other words, if the current voxel V itself is not stable (meaning _toppledir contains any value different than -1) it means that one 'grain of sand' is going to topple , decreasing V's Height.
Let's implement Step 2 in Houdini : drop a new volumewrangle node and get the data about the 4 adjacent voxels.
The first 4 lines should be familiar. We're fetching the current voxel's adjacent voxels content for the grid
_toppledir that we populated in step 1.
In line 5, I'm just fetching topple_threshold stored in step 1.
Why am I dividing it by 4 ? I'll explain it in a moment.
Cool, now we know in what direction the adjacent voxels will topple. Now we need to check if any of the adjacent stacks are going to topple on the current voxel. In that case we need to increase the current voxel's
Height by the
topple_threshold.
Let's remember that
topple_threshold is the threshold value that decides if a voxel is unstable. So , in step 2, if all 4 the adjacent voxels are toppling towards the current voxel, it means that the current voxel's
Height will be increased by topple_threshold*4.
Now, this wouldn't be 'fair' towards the adjacent voxels, because in Step 1, each one of them alone had a reason to topple on the current voxel. If when an adjacent stack topples on the current voxel I increase it by the *whole* topple_threshold amount, this alone would be enough to re-evaluate the reasons for the remaining voxels to topple on the current voxels. We need, instead, to preserve the consistency with the decisions made in Step 1. This is why I'm dividing the value by 4.0.
This way, if all the adjacent stacks topple towards the current stack , Height will never get higher than any of those adjacent stacks.
Cool, all we need to do, is to check if the adjacent stacks have any intention to topple on the current stack. In other words ...
- if the stack on the right wants to topple on the left increase the current stack by threshold/4
- if the stack on the left wants to topple on the right increase the current stack by threshold/4
- if the stack up wants to topple down increase the current stack by threshold/4
- if the stack down wants to topple up increase the current stack by threshold/4
... that's not it yet. We need to check if the current stack is not stable ..
- if the current stack wants to topple (we don't care where) decrease the current stack by threshold/4
Let's write all this in VEX :
... first off I'm initializing to zero a new variable height_incr where I want to store the toppling contributions coming from all the directions.
All the if... statements are doing exactly what I described earlier.
- if (dxp == 3) ...
means ... if the stack on the right (xp = x positive) wants to topple towards the left (remember that according to our convention in Fig.1 the number 3 means 'left').
- if (dxn == 1) ...
means ... if the stack on the right (xn = x negative) wants to
topple towards the right (remember that according to our convention in
Fig.1 the number 1 means 'right').
- ...
- if (f@_toppledir!=-1)
means ... if the current voxel is not stable (meaning _toppledir does not contain -1) then , regardless of what direction it'll topple, has to go down, decrease.
After accumulating all the sand contribution in
height_incr , I'll add it to the current height (last line).
Done. Finish. Caput. Finito.
Almost.
Ok to recap this is what your network should look like
This is the vex code contained in 'step1' Point Wrangle node:
And this is the code contained in 'step2' Point Wrangle node:
Cool.
Now, if you check your bloody napk .. uhm your sand distribution in the viewport, not much is changed. Well, check better ... it is actually changed, but veeery very little. You need to really zoom in a detail, and if you enable and disable the node 'step2' you'll notice that something is actually changing.
This happens of course because this is only one iteration. We need to repeat this process over and over in order to see the something interesting, and of course Solver SOP is once again our friend.
All we need to do is move the nodes step1 and step2 in a Solver SOP. The Solver SOP will fetch the geometry only at the frame specified in the parameter Start Frame (typically frame 1). For all the subsequent frames, the Solver will use the result of the previous iteration. In other words, will perform a 'Feedback Loop'.
Let's do that.
- Create a Solver SOP node, and copy and paste the nodes step1 and step2 inside the Solver SOP network.
- inside the Solver SOP network connect Prev_Frame input to the node step1
- inside the Solver SOP , change the expression on the node step2 to
ch("../../../../heightfield1/gridspacing")
- inside the Solver SOP, on the node step 1 change the parameter Topple Threshold Mult to 2. This will make sure that only the very steep parts of the sand distribution will be modified, which is more realistic.
- outside of the Solver SOP connect the node heightfield_noise1 with input 1 of the Solver SOP.
- outside of the Solver SOP connect the output of the Solver SOP to a delete node, and use it to delete the field '__toppledir'.
This field was only a temporary storage to store data between step1 and step2. Once we're out of the Solver SOP we no longer need it.
- outside of the Solver SOP, Set the number of Sub Steps to 20.
Make sure you're on Frame 1 , and in your ViewPort you should see something like this :
Notice that the mask field is marking in red what elements of the sand distribution are not stable.
Let's press play and see what happens.
It's cool to see how the unstable sand areas get smaller and smaller , that is comforting cause it means the sand distribution is adapting to find a stable state. Let's remove the red areas, so we can actually see the result of all our work.
In the delete node, append
@name=mask to the Group parameter to remove the mask feedback from the viewport.